Difference between revisions of "Modeling Human Performance"
User:Fellrnr (User talk:Fellrnr | contribs) (Created page with "Training Stress Balance (TSB) is a method for evaluating the effect of training over time. This approach assumes that given training stress, also known as "training impulse" or [...") |
User:Fellrnr (User talk:Fellrnr | contribs) |
||
| Line 13: | Line 13: | ||
=Flaws in the TSB model= | =Flaws in the TSB model= | ||
| − | The first flaw in the TSB model is that it ignores [[Overtraining]] | + | There are a number of practical flaws in the TSB model. |
| − | + | * The first flaw in the TSB model is that it ignores [[Overtraining]] and predicts that any possible workload produces improved fitness. Related to this problem is that the model ignores [[Training Monotony]]. Research has shown that training with a high level of monotony reduces the benefits and increases the fatigue from a given level of training. | |
| + | * The second flaw is that the values for the constants used in the model are specific to each individual, and possibly to the particular training regime. The verification of the model reverse engineered the constants so that the model accurately predicted the performance changes. These constants are represented below as | ||
| + | ** N<sub>a</sub> - the decay constant for acute (fatigue) effect of training. | ||
| + | ** N<sub>f</sub> - the decay constant for fitness effect of training. | ||
| + | ** K<sub>a</sub> - the scaling constant for acute (fatigue) effect of training | ||
| + | ** K<sub>f</sub> - the scaling constant for fitness effect of training. | ||
| + | ** The ratio of K<sub>a</sub> to K<sub>f</sub> defines the benefit of training. If they are both the same value, then you get no benefit from training, but if K<sub>a</sub> is larger than K<sub>f</sub> then training improves your performance over time. | ||
=An Advanced TSB= | =An Advanced TSB= | ||
One approach to addressing these flaws is to use the calculated [[Training Monotony]] to change the TSB calculation. Higher levels of monotony should reduce the CTL value, increase the ATL value, and increase the time constant used to reduce the effect of a workout on ATL. I've built this into my [[SportTracks Dailymile Plugin]]. | One approach to addressing these flaws is to use the calculated [[Training Monotony]] to change the TSB calculation. Higher levels of monotony should reduce the CTL value, increase the ATL value, and increase the time constant used to reduce the effect of a workout on ATL. I've built this into my [[SportTracks Dailymile Plugin]]. | ||
Revision as of 15:29, 26 November 2012
Training Stress Balance (TSB) is a method for evaluating the effect of training over time. This approach assumes that given training stress, also known as "training impulse" or TRIMP (TRaining IMPulse), has both a positive and a negative effect. The positive effect could be considered "fitness", and the negative effect could be considered "fatigue." The positive effect is called Chronic Training Load (CTL) and the negative effect is called Acute Training Load (ATL). Both CTL and ATL are based on TRIMP, with the effect of a given workout reducing over time, but the effect lasts longer on CTL than on ATL. In addition the TSB method assumes the effect is greater on CTL than on ATL.
Contents
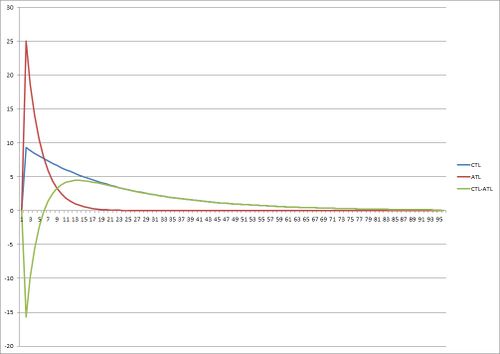
[hide]1 TSB For a Single Workout
The image above shows the effect of a single workout on the Training Stress Balance. You can see the workout creates a peak in both ATL and CTL. The peak is greater ATL, but reduces more quickly than in CTL. The Training Stress Balance is CTL-ATL, and you can see it initially go negative indicating a reduced ability to perform, then rises to be positive as CTL becomes greater than ATL. This green TSB line is the same as that seen in Supercompensation.
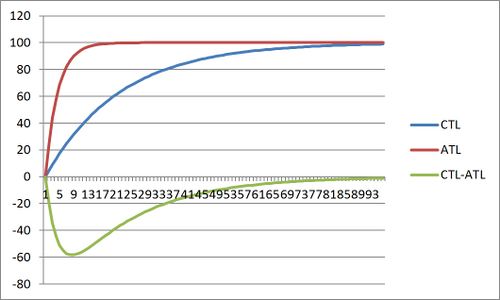
2 TSB for Multiple Workouts
The effect of a continuous series of identical workouts on TSB is shown in the image above. The ATL rises sharply and reaches a steady-state, with CTL rising more slowly to a greater level. The TSB (CTL-ATL) initially goes negative, but rises towards a positive steady-state.
3 The value of the TSB model
The TSB model can provide an estimation of how changes in training load affect fatigue and performance. A positive TSB indicates improved performance.
4 Flaws in the TSB model
There are a number of practical flaws in the TSB model.
- The first flaw in the TSB model is that it ignores Overtraining and predicts that any possible workload produces improved fitness. Related to this problem is that the model ignores Training Monotony. Research has shown that training with a high level of monotony reduces the benefits and increases the fatigue from a given level of training.
- The second flaw is that the values for the constants used in the model are specific to each individual, and possibly to the particular training regime. The verification of the model reverse engineered the constants so that the model accurately predicted the performance changes. These constants are represented below as
- Na - the decay constant for acute (fatigue) effect of training.
- Nf - the decay constant for fitness effect of training.
- Ka - the scaling constant for acute (fatigue) effect of training
- Kf - the scaling constant for fitness effect of training.
- The ratio of Ka to Kf defines the benefit of training. If they are both the same value, then you get no benefit from training, but if Ka is larger than Kf then training improves your performance over time.
5 An Advanced TSB
One approach to addressing these flaws is to use the calculated Training Monotony to change the TSB calculation. Higher levels of monotony should reduce the CTL value, increase the ATL value, and increase the time constant used to reduce the effect of a workout on ATL. I've built this into my SportTracks Dailymile Plugin.
6 Calculation Details
Understanding these details is not required for using the TSB, but you may find them interesting.
6.1 The basic formula
The basic formula for calculating ATL/CTL uses an Exponential moving average that is calculated like this:
ATLtoday = TRIMP * λa * ka + ((1 – λa) * ATLyesterday CTLtoday = TRIMP * λf * kf + ((1 – λf) * CTLyesterday
As you can see this is an iterative approach, calculating the value for the oldest workout, then iterating through each subsequent workout.
6.1.1 Lambda
The calculation for λa and λf is:
λa = 2/(Na+1) λf = 2/(Nf+1)
Where Na and Nf are the time decay constants, normally 7 and 42 days respectively. The half-life for a given value of N is N/2.8854, so 7 days gives a half-life of 2.4 days and 42 days is 14.5 days.
6.1.2 Scaling Factors
The values ka and kf are the scaling factors for fatigue and fitness respectively. Normally ka is set to 1 and kf is set to 2, meaning that a workout produces twice as much fitness as fatigue.
6.2 Adjusting for Monotony
The calculation of Monotony is covered in Training Monotony. The modified calculation for ATLm (ATLmonotony) and CTLm (CTLmonotony):
ATLmtoday = TRIMPam * λma * ka + ((1 – λma) * ATLmyesterday CTLmtoday = TRIMPcm * λf * kf + ((1 – λmc) * CTLmyesterday
6.2.1 Modified TRIMP
The value of TRIMP is modified by monotony:
TRIMPam = (TRIMP *MonotonyRatio * ATLmStressPercent) + (TRIMP * (1 - ATLmStressPercent)) TRIMPcm = (TRIMP *MonotonyRatio * CTLmStressPercent) + (TRIMP * (1 - CTLmStressPercent))
The ATLmStressPercent and CTLmStressPercent are how much of the monotony modification to apply, which defaults to 50% (0.5).
6.2.2 MonotonyRatio
Using raw monotony tends to have an overly large impact. Instead, the concept of a 'monotony break even' is used, which is the monotony level that an athlete has no negative effects. This defaults to 1.5. In addition, higher levels of monotony tend to produce unreasonably high monotony values, so monotony is capped, by default at 4.0. The MonotonyRatio is then:
MonotonyRatio = min(Monotony, MonotonyCap) / MonotonyBreakEven
6.2.3 Adjusting Fatigue Lambda
Because Training Monotony increases the time that fatigue lasts for, the value of λa is modified to create λma:
λma = λa * MonotonyRatio * ATLmLambdaPercent + (λa * (1 - ATLmLambdaPercent))
The ATLmLambdaPercent is how much of the monotony modification to apply, which defaults to 50% (0.5).